MIMO with MMSE equalizer
In a previous post, we had discussed a 2×2 MIMO transmission using BPSK modulation in Rayleigh channel with a Zero Forcing equalizer. The simulated results with the 2×2 MIMO system with zero forcing equalizer showed matching results as obtained in for a 1×1 system for BPSK modulation in Rayleigh channel. In this post, we will discuss a different equalization approach called Minimum Mean Square Error (MMSE) equalization. We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.
The background material on the MIMO channel has been described in the post on Zero Forcing equalizer. The text is repeated again for easy readability.
2×2 MIMO channel
In a 2×2 MIMO channel, probable usage of the available 2 transmit antennas can be as follows:
1. Consider that we have a transmission sequence, for example
2. In normal transmission, we will be sending in the first time slot,
in the second time slot,
and so on.
3. However, as we now have 2 transmit antennas, we may group the symbols into groups of two. In the first time slot, send and
from the first and second antenna. In second time slot, send
and
from the first and second antenna, send
and
in the third time slot and so on.
4. Notice that as we are grouping two symbols and sending them in one time slot, we need only time slots to complete the transmission – data rate is doubled !
![]()
5. This forms the simple explanation of a probable MIMO transmission scheme with 2 transmit antennas and 2 receive antennas.
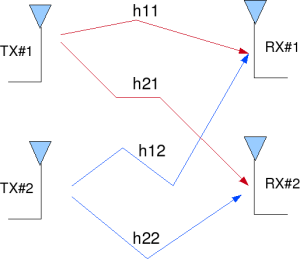
Figure: 2 Transmit 2 Receive (2×2) MIMO channel
Other Assumptions
1. The channel is flat fading – In simple terms, it means that the multipath channel has only one tap. So, the convolution operation reduces to a simple multiplication. For a more rigorous discussion on flat fading and frequency selective fading, may I urge you to review Chapter 15.3 Signal Time-Spreading from [DIGITAL COMMUNICATIONS: SKLAR]
2. The channel experience by each transmit antenna is independent from the channel experienced by other transmit antennas.
3. For the transmit antenna to
receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number
. As the channel under consideration is a Rayleigh channel, the real and imaginary parts of
are Gaussian distributed having mean
and variance
.
4. The channel experienced between each transmit to the receive antenna is independent and randomly varying in time.
5. On the receive antenna, the noise has the Gaussian probability density function with
with
and
.
7. The channel is known at the receiver.
Minimum Mean Square Error (MMSE) equalizer for 2×2 MIMO channel
Let us now try to understand the math for extracting the two symbols which interfered with each other. In the first time slot, the received signal on the first receive antenna is,
.
The received signal on the second receive antenna is,
.
where
,
are the received symbol on the first and second antenna respectively,
is the channel from
transmit antenna to
receive antenna,
is the channel from
transmit antenna to
receive antenna,
is the channel from
transmit antenna to
receive antenna,
is the channel from
transmit antenna to
receive antenna,
,
are the transmitted symbols and
is the noise on
receive antennas.
We assume that the receiver knows ,
,
and
. The receiver also knows
and
. For convenience, the above equation can be represented in matrix notation as follows:
.
Equivalently,
The Minimum Mean Square Error (MMSE) approach tries to find a coefficient which minimizes the criterion,
.
Solving,
.
When comparing to the equation in Zero Forcing equalizer, apart from the term both the equations are comparable. Infact, when the noise term is zero, the MMSE equalizer reduces to Zero Forcing equalizer.
Simulation Model
The Matlab/Octave script performs the following
(a) Generate random binary sequence of +1’s and -1’s.
(b) Group them into pair of two symbols and send two symbols in one time slot
(c) Multiply the symbols with the channel and then add white Gaussian noise.
(d) Equalize the received symbols
(e) Perform hard decision decoding and count the bit errors
(f) Repeat for multiple values of and plot the simulation and theoretical results.
Click here to download Matlab/Octave script for simulating BER in a 2×2 MIMO channel with MMSE equalization for BPSK in Rayleigh channel

Figure: BER plot for 2×2 MIMO with MMSE equalization for BPSK in Rayleigh channel
Summary
Compared to the Zero Forcing equalizer case, at BER point, it can be seen that the Minimum Mean Square Error (MMSE) equalizer results in around 3dB of improvement.
![]()
References
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt
[WIRELESS-TSE, VISWANATH] Fundamentals of Wireless Communication, David Tse, Pramod Viswanath
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% All rights reserved by Krishna Pillai, http://www.dsplog.com
% The file may not be re-distributed without explicit authorization
% from Krishna Pillai.
% Checked for proper operation with Octave Version 3.0.0
% Author : Krishna Pillai
% Email : krishna@dsplog.com
% Version : 1.0
% Date : 02nd Novemeber 2008
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Script for computing the BER for BPSK modulation in a
% Rayleigh fading channel with 2 Tx, 2Rx MIMO channel
% Minimum Mean Square Error equalization
clear
N = 10^6; % number of bits or symbols
Eb_N0_dB = [0:25]; % multiple Eb/N0 values
nTx = 2;
nRx = 2;
for ii = 1:length(Eb_N0_dB)
% Transmitter
ip = rand(1,N)>0.5; % generating 0,1 with equal probability
s = 2*ip-1; % BPSK modulation 0 -> -1; 1 -> 0
sMod = kron(s,ones(nRx,1)); %
sMod = reshape(sMod,[nRx,nTx,N/nTx]); % grouping in [nRx,nTx,N/NTx ] matrix
h = 1/sqrt(2)*[randn(nRx,nTx,N/nTx) + j*randn(nRx,nTx,N/nTx)]; % Rayleigh channel
n = 1/sqrt(2)*[randn(nRx,N/nTx) + j*randn(nRx,N/nTx)]; % white gaussian noise, 0dB variance
% Channel and noise Noise addition
y = squeeze(sum(h.*sMod,2)) + 10^(-Eb_N0_dB(ii)/20)*n;
% Receiver
% Forming the MMSE equalization matrix W = inv(H^H*H+sigma^2*I)*H^H
% H^H*H is of dimension [nTx x nTx]. In this case [2 x 2]
% Inverse of a [2x2] matrix [a b; c d] = 1/(ad-bc)[d -b;-c a]
hCof = zeros(2,2,N/nTx) ;
hCof(1,1,:) = sum(h(:,2,:).*conj(h(:,2,:)),1) + 10^(-Eb_N0_dB(ii)/10); % d term
hCof(2,2,:) = sum(h(:,1,:).*conj(h(:,1,:)),1) + 10^(-Eb_N0_dB(ii)/10); % a term
hCof(2,1,:) = -sum(h(:,2,:).*conj(h(:,1,:)),1); % c term
hCof(1,2,:) = -sum(h(:,1,:).*conj(h(:,2,:)),1); % b term
hDen = ((hCof(1,1,:).*hCof(2,2,:)) - (hCof(1,2,:).*hCof(2,1,:))); % ad-bc term
hDen = reshape(kron(reshape(hDen,1,N/nTx),ones(2,2)),2,2,N/nTx); % formatting for division
hInv = hCof./hDen; % inv(H^H*H)
hMod = reshape(conj(h),nRx,N); % H^H operation
yMod = kron(y,ones(1,2)); % formatting the received symbol for equalization
yMod = sum(hMod.*yMod,1); % H^H * y
yMod = kron(reshape(yMod,2,N/nTx),ones(1,2)); % formatting
yHat = sum(reshape(hInv,2,N).*yMod,1); % inv(H^H*H)*H^H*y
% receiver - hard decision decoding
ipHat = real(yHat)>0;
% counting the errors
nErr(ii) = size(find([ip- ipHat]),2);
end
simBer = nErr/N; % simulated ber
EbN0Lin = 10.^(Eb_N0_dB/10);
theoryBer_nRx1 = 0.5.*(1-1*(1+1./EbN0Lin).^(-0.5));
p = 1/2 - 1/2*(1+1./EbN0Lin).^(-1/2);
theoryBerMRC_nRx2 = p.^2.*(1+2*(1-p));
close all
figure
semilogy(Eb_N0_dB,theoryBer_nRx1,'bp-','LineWidth',2);
hold on
semilogy(Eb_N0_dB,theoryBerMRC_nRx2,'kd-','LineWidth',2);
semilogy(Eb_N0_dB,simBer,'mo-','LineWidth',2);
axis([0 25 10^-5 0.5])
grid on
legend('theory (nTx=2,nRx=2, ZF)', 'theory (nTx=1,nRx=2, MRC)', 'sim (nTx=2, nRx=2, MMSE)');
xlabel('Average Eb/No,dB');
ylabel('Bit Error Rate');
title('BER for BPSK modulation with 2x2 MIMO and MMSE equalizer (Rayleigh channel)');
 评论 (0)
评论 (0)