Six equalizers for V-BLAST
In the past, we had discussed several posts on two transmit two receive MIMO communication, where the transmission was based on V-BLAST. The details about V-BLAST can be read from the landmark paper V-BLAST: An architeture for realizing very high data rates over the rich scattering wireless channel – P. W. Wolniansky, G. J. Foschini, G. D. Golden, R. A. Valenzuela. We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.
Figure: 2 transmit 2 receive MIMO channel
V-BLAST transmission for 2×2 MIMO channel
In a 2×2 MIMO channel, probable usage of the available 2 transmit antennas can be as follows:
1. Consider that we have a transmission sequence, for example
2. In normal transmission, we will be sending in the first time slot,
in the second time slot,
and so on.
3. However, as we now have 2 transmit antennas, we may group the symbols into groups of two. In the first time slot, send and
from the first and second antenna. In second time slot, send
and
from the first and second antenna, send
and
in the third time slot and so on.
4. Notice that as we are grouping two symbols and sending them in one time slot, we need only time slots to complete the transmission – data rate is doubled !
![]()
5. This forms the simple explanation of a probable MIMO transmission scheme with 2 transmit antennas and 2 receive antennas.
Other Assumptions
1. The channel is flat fading – In simple terms, it means that the multipath channel has only one tap. So, the convolution operation reduces to a simple multiplication. For a more rigorous discussion on flat fading and frequency selective fading, may I urge you to review Chapter 15.3 Signal Time-Spreading from [DIGITAL COMMUNICATIONS: SKLAR]
2. The channel experience by each transmit antenna is independent from the channel experienced by other transmit antennas.
3. For the transmit antenna to
receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number
. As the channel under consideration is a Rayleigh channel, the real and imaginary parts of
are Gaussian distributed having mean
and variance
.
4. The channel experienced between each transmit to the receive antenna is independent and randomly varying in time.
5. On the receive antenna, the noise has the Gaussian probability density function with
with
and
.
7. The channel is known at the receiver.
System Model
The received signal on the first receive antenna is,
.
The received signal on the second receive antenna is,
.
where
,
are the received symbol on the first and second antenna respectively,
is the channel from
transmit antenna to
receive antenna,
is the channel from
transmit antenna to
receive antenna,
is the channel from
transmit antenna to
receive antenna,
is the channel from
transmit antenna to
receive antenna,
,
are the transmitted symbols and
is the noise on
receive antennas.
We assume that the receiver knows ,
,
and
. The receiver also knows
and
. The unknown s are
and
. Two equations and two unknowns. Can we solve it? Answer is YES.
![]()
For convenience, the above equation can be represented in matrix notation as follows:
.
Equivalently,
Receiver structures
MIMO with Zero Forcing Equalization
The zero forcing approach tries to find a matrix which satisfies
. The Zero Forcing (ZF) linear detector for meeting this constraint is given by,
.
MIMO with MMSE Equalization
The Minimum Mean Square Error (MMSE) approach tries to find a coefficient which minimizes the criterion,
.
Solving,
.
Zero Forcing Equalization with Successive Interference Cancellation
Using the Zero Forcing (ZF) equalization approach described above, the receiver can obtain an estimate of the two transmitted symbols ,
, i.e.
.
Take one of the estimated symbols (for example ) and subtract its effect from the received vector
and
, i.e.
.
Expressing in matrix notation,
,
The above equation is same as equation obtained for receive diversity case. Optimal way of combining the information from multiple copies of the received symbols in receive diversity case is to apply Maximal Ratio Combining (MRC).
The equalized symbol is,
.
This forms the simple explanation for Zero Forcing Equalizer with Successive Interference Cancellation (ZF-SIC) approach.
Zero Forcing Equalization with Optimally ordered Successive Interference Cancellation
In classical Successive Interference Cancellation, the receiver arbitrarily takes one of the estimated symbols, and subtract its effect from the received symbol and
. However, we can have more intelligence in choosing whether we should subtract the effect of
first or
first. To make that decision, let us find out the transmit symbol (after multiplication with the channel) which came at higher power at the receiver. The received power at the both the antennas corresponding to the transmitted symbol
is,
.
The received power at the both the antennas corresponding to the transmitted symbol is,
.
If then the receiver decides to remove the effect of
from the received vector
and
and then re-estimate
. Else if
the receiver decides to subtract effect of
from the received vector
and
, and then re-estimate
.
MMSE equalization with optimaly ordered Successive Interference Cancellation
Using the Minimum Mean Square Error (MMSE) equalization, the receiver can obtain an estimate of the two transmitted symbols ,
, i.e.
.
If then the receiver decides to remove the effect of
from the received vector
and
. Else if
the receiver decides to subtract effect of
from the received vector
and
, and then re-estimate
.
Once the effect of either or
is removed, the new channel becomes a one transmit antenna, 2 receive antenna case and the symbol on the other spatial dimension can be optimally equalized by Maximal Ratio Combining (MRC).
MIMO with ML equalization
The Maximum Likelihood receiver tries to find which minimizes,
Since the modulation is BPSK, the possible values of is +1 or -1 Similarly
also take values +1 or -1. So, to find the Maximum Likelihood solution, we need to find the minimum from the all four combinations of
and
.
The estimate of the transmit symbol is chosen based on the minimum value from the above four values i.e
if the minimum is ,
if the minimum is ,
if the minimum is and
if the minimum is .
Simulation Results
The plot embedded below captures BER for 2 transmit 2 receive MIMO V-BLAST ttansmission/reception for BPSK modulation in a flat fading independent Rayleigh channel, for the different equalizer structures discussed above.
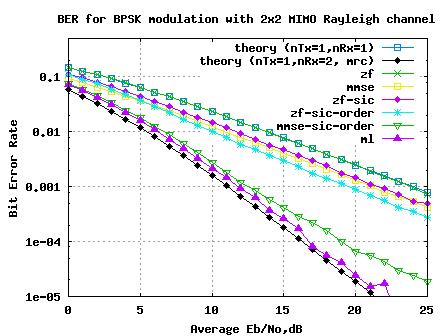
Figure: BER plot for 2 transmit 2 receive MIMO channel for BPSK modulation
Observations
1. The BER curve with ZF equalization for 2×2 MIMO channel is identical to BER plot for 1 transmit 1 receive system
2. Ordered variant of successive interference cancellation shows better performance than the simple successive interference cancellation
3. MMSE equalization with ordered successive interference cancellation provides performance which is slightly poorer than ML.
4. With ML equalization, we come close to the performance of 1 transmit 2 receive MRC case. We gain both throughput gain and diversity gain.
Reference
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt