In a previous post, we had discussed a 2×2 MIMO transmission using BPSK modulation in Rayleigh channel with a Zero Forcing equalizer. The simulated results with the 2×2 MIMO system with zero forcing equalizer showed matching results as obtained in for a 1×1 system for BPSK modulation in Rayleigh channel. In this post, we will discuss a different equalization approach called Minimum Mean Square Error (MMSE) equalization. We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.
The background material on the MIMO channel has been described in the post on Zero Forcing equalizer. The text is repeated again for easy readability.
2×2 MIMO channel
In a 2×2 MIMO channel, probable usage of the available 2 transmit antennas can be as follows:
1. Consider that we have a transmission sequence, for example 
2. In normal transmission, we will be sending  in the first time slot,
in the first time slot,  in the second time slot,
in the second time slot,  and so on.
and so on.
3. However, as we now have 2 transmit antennas, we may group the symbols into groups of two. In the first time slot, send  and
and  from the first and second antenna. In second time slot, send
from the first and second antenna. In second time slot, send  and
and  from the first and second antenna, send
from the first and second antenna, send  and
and  in the third time slot and so on.
in the third time slot and so on.
4. Notice that as we are grouping two symbols and sending them in one time slot, we need only  time slots to complete the transmission – data rate is doubled !
time slots to complete the transmission – data rate is doubled ! 
5. This forms the simple explanation of a probable MIMO transmission scheme with 2 transmit antennas and 2 receive antennas.
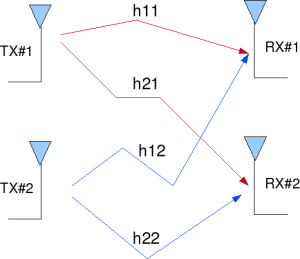
Figure: 2 Transmit 2 Receive (2×2) MIMO channel
Other Assumptions
1. The channel is flat fading – In simple terms, it means that the multipath channel has only one tap. So, the convolution operation reduces to a simple multiplication. For a more rigorous discussion on flat fading and frequency selective fading, may I urge you to review Chapter 15.3 Signal Time-Spreading from [DIGITAL COMMUNICATIONS: SKLAR]
2. The channel experience by each transmit antenna is independent from the channel experienced by other transmit antennas.
3. For the  transmit antenna to
transmit antenna to  receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number
receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number  . As the channel under consideration is a Rayleigh channel, the real and imaginary parts of
. As the channel under consideration is a Rayleigh channel, the real and imaginary parts of  are Gaussian distributed having mean
are Gaussian distributed having mean  and variance
and variance  .
.
4. The channel experienced between each transmit to the receive antenna is independent and randomly varying in time.
5. On the receive antenna, the noise has the Gaussian probability density function with
has the Gaussian probability density function with
 with
with  and
and  .
.
7. The channel  is known at the receiver.
is known at the receiver.
Minimum Mean Square Error (MMSE) equalizer for 2×2 MIMO channel
Let us now try to understand the math for extracting the two symbols which interfered with each other. In the first time slot, the received signal on the first receive antenna is,
 .
.
The received signal on the second receive antenna is,
 .
.
where
 ,
,  are the received symbol on the first and second antenna respectively,
are the received symbol on the first and second antenna respectively,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 ,
,  are the transmitted symbols and
are the transmitted symbols and
 is the noise on
is the noise on  receive antennas.
receive antennas.
We assume that the receiver knows  ,
,  ,
,  and
and  . The receiver also knows
. The receiver also knows  and
and  . For convenience, the above equation can be represented in matrix notation as follows:
. For convenience, the above equation can be represented in matrix notation as follows:
 .
.
Equivalently,

The Minimum Mean Square Error (MMSE) approach tries to find a coefficient  which minimizes the criterion,
which minimizes the criterion,
 .
.
Solving,
 .
.
When comparing to the equation in Zero Forcing equalizer, apart from the  term both the equations are comparable. Infact, when the noise term is zero, the MMSE equalizer reduces to Zero Forcing equalizer.
term both the equations are comparable. Infact, when the noise term is zero, the MMSE equalizer reduces to Zero Forcing equalizer.
Simulation Model
The Matlab/Octave script performs the following
(a) Generate random binary sequence of +1’s and -1’s.
(b) Group them into pair of two symbols and send two symbols in one time slot
(c) Multiply the symbols with the channel and then add white Gaussian noise.
(d) Equalize the received symbols
(e) Perform hard decision decoding and count the bit errors
(f) Repeat for multiple values of  and plot the simulation and theoretical results.
and plot the simulation and theoretical results.
Click here to download Matlab/Octave script for simulating BER in a 2×2 MIMO channel with MMSE equalization for BPSK in Rayleigh channel

Figure: BER plot for 2×2 MIMO with MMSE equalization for BPSK in Rayleigh channel
Summary
Compared to the Zero Forcing equalizer case, at  BER point, it can be seen that the Minimum Mean Square Error (MMSE) equalizer results in around 3dB of improvement.
BER point, it can be seen that the Minimum Mean Square Error (MMSE) equalizer results in around 3dB of improvement. 
References
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt
[WIRELESS-TSE, VISWANATH] Fundamentals of Wireless Communication, David Tse, Pramod Viswanath
Fundamentals of Wireless Communication, David Tse, Pramod Viswanath
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% All rights reserved by Krishna Pillai, http://www.dsplog.com
% The file may not be re-distributed without explicit authorization
% from Krishna Pillai.
% Checked for proper operation with Octave Version 3.0.0
% Author : Krishna Pillai
% Email : krishna@dsplog.com
% Version : 1.0
% Date : 02nd Novemeber 2008
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Script for computing the BER for BPSK modulation in a
% Rayleigh fading channel with 2 Tx, 2Rx MIMO channel
% Minimum Mean Square Error equalization
clear
N = 10^6; % number of bits or symbols
Eb_N0_dB = [0:25]; % multiple Eb/N0 values
nTx = 2;
nRx = 2;
for ii = 1:length(Eb_N0_dB)
% Transmitter
ip = rand(1,N)>0.5; % generating 0,1 with equal probability
s = 2*ip-1; % BPSK modulation 0 -> -1; 1 -> 0
sMod = kron(s,ones(nRx,1)); %
sMod = reshape(sMod,[nRx,nTx,N/nTx]); % grouping in [nRx,nTx,N/NTx ] matrix
h = 1/sqrt(2)*[randn(nRx,nTx,N/nTx) + j*randn(nRx,nTx,N/nTx)]; % Rayleigh channel
n = 1/sqrt(2)*[randn(nRx,N/nTx) + j*randn(nRx,N/nTx)]; % white gaussian noise, 0dB variance
% Channel and noise Noise addition
y = squeeze(sum(h.*sMod,2)) + 10^(-Eb_N0_dB(ii)/20)*n;
% Receiver
% Forming the MMSE equalization matrix W = inv(H^H*H+sigma^2*I)*H^H
% H^H*H is of dimension [nTx x nTx]. In this case [2 x 2]
% Inverse of a [2x2] matrix [a b; c d] = 1/(ad-bc)[d -b;-c a]
hCof = zeros(2,2,N/nTx) ;
hCof(1,1,:) = sum(h(:,2,:).*conj(h(:,2,:)),1) + 10^(-Eb_N0_dB(ii)/10); % d term
hCof(2,2,:) = sum(h(:,1,:).*conj(h(:,1,:)),1) + 10^(-Eb_N0_dB(ii)/10); % a term
hCof(2,1,:) = -sum(h(:,2,:).*conj(h(:,1,:)),1); % c term
hCof(1,2,:) = -sum(h(:,1,:).*conj(h(:,2,:)),1); % b term
hDen = ((hCof(1,1,:).*hCof(2,2,:)) - (hCof(1,2,:).*hCof(2,1,:))); % ad-bc term
hDen = reshape(kron(reshape(hDen,1,N/nTx),ones(2,2)),2,2,N/nTx); % formatting for division
hInv = hCof./hDen; % inv(H^H*H)
hMod = reshape(conj(h),nRx,N); % H^H operation
yMod = kron(y,ones(1,2)); % formatting the received symbol for equalization
yMod = sum(hMod.*yMod,1); % H^H * y
yMod = kron(reshape(yMod,2,N/nTx),ones(1,2)); % formatting
yHat = sum(reshape(hInv,2,N).*yMod,1); % inv(H^H*H)*H^H*y
% receiver - hard decision decoding
ipHat = real(yHat)>0;
% counting the errors
nErr(ii) = size(find([ip- ipHat]),2);
end
simBer = nErr/N; % simulated ber
EbN0Lin = 10.^(Eb_N0_dB/10);
theoryBer_nRx1 = 0.5.*(1-1*(1+1./EbN0Lin).^(-0.5));
p = 1/2 - 1/2*(1+1./EbN0Lin).^(-1/2);
theoryBerMRC_nRx2 = p.^2.*(1+2*(1-p));
close all
figure
semilogy(Eb_N0_dB,theoryBer_nRx1,'bp-','LineWidth',2);
hold on
semilogy(Eb_N0_dB,theoryBerMRC_nRx2,'kd-','LineWidth',2);
semilogy(Eb_N0_dB,simBer,'mo-','LineWidth',2);
axis([0 25 10^-5 0.5])
grid on
legend('theory (nTx=2,nRx=2, ZF)', 'theory (nTx=1,nRx=2, MRC)', 'sim (nTx=2, nRx=2, MMSE)');
xlabel('Average Eb/No,dB');
ylabel('Bit Error Rate');
title('BER for BPSK modulation with 2x2 MIMO and MMSE equalizer (Rayleigh channel)');
We have discussed quite a few receiver structures for a 2×2 MIMO channel namely,
(a) Zero Forcing (ZF) equalization
(b) Minimum Mean Square Error (MMSE) equalization
(c) Zero Forcing equalization with Successive Interference Cancellation (ZF-SIC)
(d) ZF-SIC with optimal ordering and
(e) MIMO with MMSE SIC and optimal ordering
From the above receiver structures, we saw that MMSE equalisation with optimally ordered Successive Interference Cancellation gave the best performance. In this post, we will discuss another receiver structure called Maximum Likelihood (ML) decoding which gives us an even better performance. We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.
2×2 MIMO channel
In a 2×2 MIMO channel, probable usage of the available 2 transmit antennas can be as follows:
1. Consider that we have a transmission sequence, for example 
2. In normal transmission, we will be sending  in the first time slot,
in the first time slot,  in the second time slot,
in the second time slot,  and so on.
and so on.
3. However, as we now have 2 transmit antennas, we may group the symbols into groups of two. In the first time slot, send  and
and  from the first and second antenna. In second time slot, send
from the first and second antenna. In second time slot, send  and
and  from the first and second antenna, send
from the first and second antenna, send  and
and  in the third time slot and so on.
in the third time slot and so on.
4. Notice that as we are grouping two symbols and sending them in one time slot, we need only  time slots to complete the transmission – data rate is doubled !
time slots to complete the transmission – data rate is doubled ! 
5. This forms the simple explanation of a probable MIMO transmission scheme with 2 transmit antennas and 2 receive antennas.

Figure: 2 Transmit 2 Receive (2×2) MIMO channel
Let us now try to understand the math for extracting the two symbols which interfered with each other. In the first time slot, the received signal on the first receive antenna is,
 .
.
The received signal on the second receive antenna is,
 .
.
where
 ,
,  are the received symbol on the first and second antenna respectively,
are the received symbol on the first and second antenna respectively,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 ,
,  are the transmitted symbols and
are the transmitted symbols and
 is the noise on
is the noise on  receive antennas.
receive antennas.
We assume that the receiver knows  ,
,  ,
,  and
and  . The receiver also knows
. The receiver also knows  and
and  . The unknown s are
. The unknown s are  and
and  .
.
For convenience, the above equation can be represented in matrix notation as follows:
 .
.
Equivalently,

Other Assumptions
1. The channel is flat fading – In simple terms, it means that the multipath channel has only one tap. So, the convolution operation reduces to a simple multiplication. For a more rigorous discussion on flat fading and frequency selective fading, may I urge you to review Chapter 15.3 Signal Time-Spreading from [DIGITAL COMMUNICATIONS: SKLAR]
2. The channel experience by each transmit antenna is independent from the channel experienced by other transmit antennas.
3. For the  transmit antenna to
transmit antenna to  receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number
receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number  . As the channel under consideration is a Rayleigh channel, the real and imaginary parts of
. As the channel under consideration is a Rayleigh channel, the real and imaginary parts of  are Gaussian distributed having mean
are Gaussian distributed having mean  and variance
and variance  .
.
4. The channel experienced between each transmit to the receive antenna is independent and randomly varying in time.
5. On the receive antenna, the noise has the Gaussian probability density function with
has the Gaussian probability density function with
 with
with  and
and  .
.
7. The channel  is known at the receiver.
is known at the receiver.
Maximum Likelihood (ML)Receiver
The Maximum Likelihood receiver tries to find  which minimizes,
which minimizes, 

Since the modulation is BPSK, the possible values of  is +1 or -1 Similarly
is +1 or -1 Similarly  also take values +1 or -1. So, to find the Maximum Likelihood solution, we need to find the minimum from the all four combinations of
also take values +1 or -1. So, to find the Maximum Likelihood solution, we need to find the minimum from the all four combinations of  and
and  .
.




The estimate of the transmit symbol is chosen based on the minimum value from the above four values i.e
if the minimum is  ,
,
if the minimum is  ,
,
if the minimum is  and
and
if the minimum is  .
.
Simulation Model
The Matlab/Octave script performs the following
(a) Generate random binary sequence of +1’s and -1’s.
(b) Group them into pair of two symbols and send two symbols in one time slot
(c) Multiply the symbols with the channel and then add white Gaussian noise.
(d) Find the minimum among the four possible transmit symbol combinations
(e) Based on the minimum chose the estimate of the transmit symbol
(h) Repeat for multiple values of  and plot the simulation and theoretical results.
and plot the simulation and theoretical results.
Click here to download Script for computing BER for BPSK in 2×2 MIMO Rayleigh channel with Maximum Likelihood Equalization
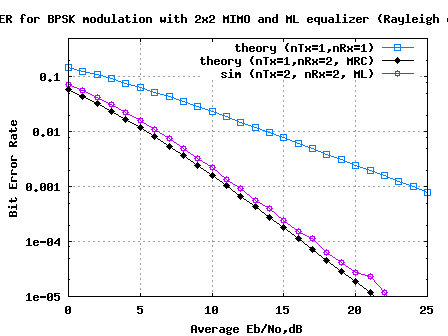
BER plot 2x2 MIMO Rayleigh channel with Maximum Likelihood equalisation
FIgure: BER plot 2×2 MIMO Rayleigh channel with Maximum Likelihood equalisation
Summary
1. The results for 2×2 MIMO with Maximum Likelihood (ML) equalization helped us to achieve a performance closely matching the 1 transmit 2 receive antenna Maximal Ratio Combining (MRC) case.
2. If we use a higher order constellation like 64QAM, then computing Maximum Likelihood equalization might become prohibitively complex. With 64QAM and 2 spatial stream we need to find the minimum from  combinations ! In such scenarios we might need to employ schemes like sphere decoding which helps to reduce the complexity.
combinations ! In such scenarios we might need to employ schemes like sphere decoding which helps to reduce the complexity.
References
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt
[WIRELESS-TSE, VISWANATH] Fundamentals of Wireless Communication, David Tse, Pramod Viswanath
Fundamentals of Wireless Communication, David Tse, Pramod Viswanath
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% All rights reserved by Krishna Pillai, http://www.dsplog.com
% The file may not be re-distributed without explicit authorization
% from Krishna Pillai.
% Checked for proper operation with Octave Version 3.0.0
% Author : Krishna Pillai
% Email : krishna@dsplog.com
% Version : 1.0
% Date : 14th December 2008
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Script for computing the BER for BPSK modulation in a
% Rayleigh fading channel with 2 Tx, 2Rx MIMO channel
% Maximum Likelihood equalization
clear
N = 10^6; % number of bits or symbols
Eb_N0_dB = [0:25]; % multiple Eb/N0 values
nTx = 2;
nRx = 2;
for ii = 1:length(Eb_N0_dB)
% Transmitter
ip = rand(1,N)>0.5; % generating 0,1 with equal probability
s = 2*ip-1; % BPSK modulation 0 -> -1; 1 -> 0
sMod = kron(s,ones(nRx,1)); %
sMod = reshape(sMod,[nRx,nTx,N/nTx]); % grouping in [nRx,nTx,N/NTx ] matrix
h = 1/sqrt(2)*[randn(nRx,nTx,N/nTx) + j*randn(nRx,nTx,N/nTx)]; % Rayleigh channel
n = 1/sqrt(2)*[randn(nRx,N/nTx) + j*randn(nRx,N/nTx)]; % white gaussian noise, 0dB variance
% Channel and noise Noise addition
y = squeeze(sum(h.*sMod,2)) + 10^(-Eb_N0_dB(ii)/20)*n;
% Maximum Likelihood Receiver
% ----------------------------
% if [s1 s2 ] = [+1,+1 ]
sHat1 = [1 1];
sHat1 = repmat(sHat1,[1 ,N/2]);
sHat1Mod = kron(sHat1,ones(nRx,1));
sHat1Mod = reshape(sHat1Mod,[nRx,nTx,N/nTx]);
zHat1 = squeeze(sum(h.*sHat1Mod,2)) ;
J11 = sum(abs(y - zHat1),1);
% if [s1 s2 ] = [+1,-1 ]
sHat2 = [1 -1];
sHat2 = repmat(sHat2,[1 ,N/2]);
sHat2Mod = kron(sHat2,ones(nRx,1));
sHat2Mod = reshape(sHat2Mod,[nRx,nTx,N/nTx]);
zHat2 = squeeze(sum(h.*sHat2Mod,2)) ;
J10 = sum(abs(y - zHat2),1);
% if [s1 s2 ] = [-1,+1 ]
sHat3 = [-1 1];
sHat3 = repmat(sHat3,[1 ,N/2]);
sHat3Mod = kron(sHat3,ones(nRx,1));
sHat3Mod = reshape(sHat3Mod,[nRx,nTx,N/nTx]);
zHat3 = squeeze(sum(h.*sHat3Mod,2)) ;
J01 = sum(abs(y - zHat3),1);
% if [s1 s2 ] = [-1,-1 ]
sHat4 = [-1 -1];
sHat4 = repmat(sHat4,[1 ,N/2]);
sHat4Mod = kron(sHat4,ones(nRx,1));
sHat4Mod = reshape(sHat4Mod,[nRx,nTx,N/nTx]);
zHat4 = squeeze(sum(h.*sHat4Mod,2)) ;
J00 = sum(abs(y - zHat4),1);
% finding the minimum from the four alphabet combinations
rVec = [J11;J10;J01;J00];
[jj dd] = min(rVec,[],1);
% mapping the minima to bits
ref = [1 1; 1 0; 0 1; 0 0 ];
ipHat = zeros(1,N);
ipHat(1:2:end) = ref(dd,1);
ipHat(2:2:end) = ref(dd,2);
% counting the errors
nErr(ii) = size(find([ip- ipHat]),2);
end
simBer = nErr/N; % simulated ber
EbN0Lin = 10.^(Eb_N0_dB/10);
theoryBer_nRx1 = 0.5.*(1-1*(1+1./EbN0Lin).^(-0.5));
p = 1/2 - 1/2*(1+1./EbN0Lin).^(-1/2);
theoryBerMRC_nRx2 = p.^2.*(1+2*(1-p));
close all
figure
semilogy(Eb_N0_dB,theoryBer_nRx1,'bp-','LineWidth',2);
hold on
semilogy(Eb_N0_dB,theoryBerMRC_nRx2,'kd-','LineWidth',2);
semilogy(Eb_N0_dB,simBer,'mo-','LineWidth',2);
axis([0 25 10^-5 0.5])
grid on
legend('theory (nTx=1,nRx=1)', 'theory (nTx=1,nRx=2, MRC)', 'sim (nTx=2, nRx=2, ML)');
xlabel('Average Eb/No,dB');
ylabel('Bit Error Rate');
title('BER for BPSK modulation with 2x2 MIMO and ML equalizer (Rayleigh channel)');
The post on MIMO with Zero Forcing equalizer discussed a probable way of equalizing a 2×2 MIMO channel. The simulated results with the 2×2 MIMO system with zero forcing equalizer showed matching results as obtained in for a 1×1 system for BPSK modulation in Rayleigh channel. In this post, we will try to improve the bit error rate performance by trying out Successive Interference Cancellation (SIC). We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.
The background material on the MIMO channel has been described in the post on Zero Forcing equalizer. The text is repeated again for easy readability.
2×2 MIMO channel
In a 2×2 MIMO channel, probable usage of the available 2 transmit antennas can be as follows:
1. Consider that we have a transmission sequence, for example 
2. In normal transmission, we will be sending  in the first time slot,
in the first time slot,  in the second time slot,
in the second time slot,  and so on.
and so on.
3. However, as we now have 2 transmit antennas, we may group the symbols into groups of two. In the first time slot, send  and
and  from the first and second antenna. In second time slot, send
from the first and second antenna. In second time slot, send  and
and  from the first and second antenna, send
from the first and second antenna, send  and
and  in the third time slot and so on.
in the third time slot and so on.
4. Notice that as we are grouping two symbols and sending them in one time slot, we need only  time slots to complete the transmission – data rate is doubled !
time slots to complete the transmission – data rate is doubled ! 
5. This forms the simple explanation of a probable MIMO transmission scheme with 2 transmit antennas and 2 receive antennas.

Figure: 2 Transmit 2 Receive (2×2) MIMO channel
Other Assumptions
1. The channel is flat fading – In simple terms, it means that the multipath channel has only one tap. So, the convolution operation reduces to a simple multiplication. For a more rigorous discussion on flat fading and frequency selective fading, may I urge you to review Chapter 15.3 Signal Time-Spreading from [DIGITAL COMMUNICATIONS: SKLAR]
2. The channel experience by each transmit antenna is independent from the channel experienced by other transmit antennas.
3. For the  transmit antenna to
transmit antenna to  receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number
receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number  . As the channel under consideration is a Rayleigh channel, the real and imaginary parts of
. As the channel under consideration is a Rayleigh channel, the real and imaginary parts of  are Gaussian distributed having mean
are Gaussian distributed having mean  and variance
and variance  .
.
4. The channel experienced between each transmit to the receive antenna is independent and randomly varying in time.
5. On the receive antenna, the noise has the Gaussian probability density function with
has the Gaussian probability density function with
 with
with  and
and  .
.
7. The channel  is known at the receiver.
is known at the receiver.
Zero forcing equalizer for 2×2 MIMO channel
Let us now try to understand the math for extracting the two symbols which interfered with each other. In the first time slot, the received signal on the first receive antenna is,
 .
.
The received signal on the second receive antenna is,
 .
.
where
 ,
,  are the received symbol on the first and second antenna respectively,
are the received symbol on the first and second antenna respectively,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 ,
,  are the transmitted symbols and
are the transmitted symbols and
 is the noise on
is the noise on  receive antennas.
receive antennas.
For convenience, the above equation can be represented in matrix notation as follows:
 .
.
Equivalently,

To solve for  , The Zero Forcing (ZF) linear detector for meeting this constraint
, The Zero Forcing (ZF) linear detector for meeting this constraint  . is given by,
. is given by,
^{-1}H^H}) .
.
To do the Successive Interference Cancellation (SIC), the receiver needs to perform the following:
Zero Forcing with Successive Interference Cancellation (ZF-SIC)
Using the Zero Forcing (ZF) equalization approach described above, the receiver can obtain an estimate of the two transmitted symbols  ,
,  , i.e.
, i.e.
^{-1}H^H}\left[\begin{array}y_1\\y_2\end{array}\right]) .
.
Take one of the estimated symbols (for example  ) and subtract its effect from the received vector
) and subtract its effect from the received vector  and
and  , i.e.
, i.e.
 .
.
Expressing in matrix notation,
 ,
,

The above equation is same as equation obtained for receive diversity case. Optimal way of combining the information from multiple copies of the received symbols in receive diversity case is to apply Maximal Ratio Combining (MRC).
The equalized symbol is,
 .
.
This forms the simple explanation for Zero Forcing Equalizer with Successive Interference Cancellation (ZF-SIC) approach.
Simulation Model
The Matlab/Octave script performs the following
(a) Generate random binary sequence of +1’s and -1’s.
(b) Group them into pair of two symbols and send two symbols in one time slot
(c) Multiply the symbols with the channel and then add white Gaussian noise.
(d) Equalize the received symbols with Zero Forcing criterion
(e) Take the symbol from the second spatial dimension, subtract from the received symbol
(f) Perform Maximal Ratio Combining for equalizing the new received symbol
(g) Perform hard decision decoding and count the bit errors
(h) Repeat for multiple values of  and plot the simulation and theoretical results.
and plot the simulation and theoretical results.
Click here to download Matlab/Octave script for simulating BER for BPSK modulation in 2×2 MIMO with Zero Forcing and Successive Interference Cancellation equalization (in Rayleigh channel)
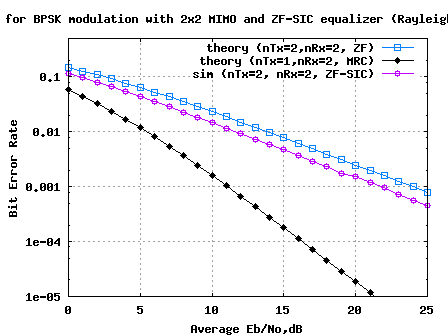
Figure: BER plot for BPSK in 2×2 MIMO channel with Zero Forcing Successive Interference Cancellation equalization
Observations
Compared to Zero Forcing equalization alone case, addition of successive interference cancellation results in around 2.2dB of improvement for BER of  .
.
The improvement is brought in because decoding of the information from the first spatial dimension ( ) has a lower error probability that the symbol transmitted from the second dimension. However, the assumption is that
) has a lower error probability that the symbol transmitted from the second dimension. However, the assumption is that  is decoded correctly may not be true in general. We can discuss alternate approaches in future posts.
is decoded correctly may not be true in general. We can discuss alternate approaches in future posts. 
References
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt
[WIRELESS-TSE, VISWANATH] Fundamentals of Wireless Communication, David Tse, Pramod Viswanath
Fundamentals of Wireless Communication, David Tse, Pramod Viswanath
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% All rights reserved by Krishna Pillai, http://www.dsplog.com
% The file may not be re-distributed without explicit authorization
% from Krishna Pillai.
% Checked for proper operation with Octave Version 3.0.0
% Author : Krishna Pillai
% Email : krishna@dsplog.com
% Version : 1.0
% Date : 09 Novemeber 2008
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Script for computing the BER for BPSK modulation in a
% Rayleigh fading channel with 2 Tx, 2Rx MIMO channel
% Zero Forcing Equalization with Successive Interference
% Cancellation (ZF-SIC)
clear
N = 10^6; % number of bits or symbols
Eb_N0_dB = [0:25]; % multiple Eb/N0 values
nTx = 2;
nRx = 2;
for ii = 1:length(Eb_N0_dB)
% Transmitter
ip = rand(1,N)>0.5; % generating 0,1 with equal probability
s = 2*ip-1; % BPSK modulation 0 -> -1; 1 -> 0
sMod = kron(s,ones(nRx,1)); %
sMod = reshape(sMod,[nRx,nTx,N/nTx]); % grouping in [nRx,nTx,N/NTx ] matrix
h = 1/sqrt(2)*[randn(nRx,nTx,N/nTx) + j*randn(nRx,nTx,N/nTx)]; % Rayleigh channel
n = 1/sqrt(2)*[randn(nRx,N/nTx) + j*randn(nRx,N/nTx)]; % white gaussian noise, 0dB variance
% Channel and noise Noise addition
y = squeeze(sum(h.*sMod,2)) + 10^(-Eb_N0_dB(ii)/20)*n;
% Receiver
% Forming the ZF equalization matrix W = inv(H^H*H)*H^H
% H^H*H is of dimension [nTx x nTx]. In this case [2 x 2]
% Inverse of a [2x2] matrix [a b; c d] = 1/(ad-bc)[d -b;-c a]
hCof = zeros(2,2,N/nTx) ;
hCof(1,1,:) = sum(h(:,2,:).*conj(h(:,2,:)),1) ; % d term
hCof(2,2,:) = sum(h(:,1,:).*conj(h(:,1,:)),1) ; % a term
hCof(2,1,:) = -sum(h(:,2,:).*conj(h(:,1,:)),1); % c term
hCof(1,2,:) = -sum(h(:,1,:).*conj(h(:,2,:)),1); % b term
hDen = ((hCof(1,1,:).*hCof(2,2,:)) - (hCof(1,2,:).*hCof(2,1,:))); % ad-bc term
hDen = reshape(kron(reshape(hDen,1,N/nTx),ones(2,2)),2,2,N/nTx); % formatting for division
hInv = hCof./hDen; % inv(H^H*H)
hMod = reshape(conj(h),nRx,N); % H^H operation
yMod = kron(y,ones(1,2)); % formatting the received symbol for equalization
yMod = sum(hMod.*yMod,1); % H^H * y
yMod = kron(reshape(yMod,2,N/nTx),ones(1,2)); % formatting
yHat = sum(reshape(hInv,2,N).*yMod,1); % inv(H^H*H)*H^H*y
% receiver - hard decision decoding on second spatial dimension
ipHat2SS = real(yHat(2:2:end))>0;
ipHatMod2SS = 2*ipHat2SS-1;
ipHatMod2SS = kron(ipHatMod2SS,ones(nRx,1));
ipHatMod2SS = reshape(ipHatMod2SS,[nRx,1,N/nTx]);
% new received symbol - removing the effect from second spatial dimension
h2SS = h(:,2,:); % channel in the second spatial dimension
r = y - squeeze(h2SS.*ipHatMod2SS);
% maximal ratio combining - for symbol in the first spatial dimension
h1SS = squeeze(h(:,1,:));
yHat1SS = sum(conj(h1SS).*r,1)./sum(h1SS.*conj(h1SS),1);
yHat(1:2:end) = yHat1SS;
% receiver - hard decision decoding
ipHat = real(yHat)>0;
% counting the errors
nErr(ii) = size(find([ip- ipHat]),2);
end
simBer = nErr/N; % simulated ber
EbN0Lin = 10.^(Eb_N0_dB/10);
theoryBer_nRx1 = 0.5.*(1-1*(1+1./EbN0Lin).^(-0.5));
p = 1/2 - 1/2*(1+1./EbN0Lin).^(-1/2);
theoryBerMRC_nRx2 = p.^2.*(1+2*(1-p));
close all
figure
semilogy(Eb_N0_dB,theoryBer_nRx1,'bp-','LineWidth',2);
hold on
semilogy(Eb_N0_dB,theoryBerMRC_nRx2,'kd-','LineWidth',2);
semilogy(Eb_N0_dB,simBer,'mo-','LineWidth',2);
axis([0 25 10^-5 0.5])
grid on
legend('theory (nTx=2,nRx=2, ZF)', 'theory (nTx=1,nRx=2, MRC)', 'sim (nTx=2, nRx=2, ZF-SIC)');
xlabel('Average Eb/No,dB');
ylabel('Bit Error Rate');
title('BER for BPSK modulation with 2x2 MIMO and ZF-SIC equalizer (Rayleigh channel)');
MIMO with ZF SIC and optimal ordering
by Krishna Sankar on November 29, 2008
In previous posts, we had discussed equalization of a 2×2 MIMO channel with Zero Forcing (ZF) equalization and later, Zero Forcing equalization with successive interference cancellation (ZF-SIC). In this post, we will explore a variant of ZF-SIC called Zero Forcing Successive Interference Cancellation with optimal ordering. We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.
Brief description of 2×2 MIMO transmission, assumptions on channel model and the noise are detailed in the post on Zero Forcing equalization with successive interference cancellation
Zero forcing equalizer for 2×2 MIMO channel
Let us now try to understand the math for extracting the two symbols which interfered with each other. In the first time slot, the received signal on the first receive antenna is,
 .
.
The received signal on the second receive antenna is,
 .
.
where
 ,
,  are the received symbol on the first and second antenna respectively,
are the received symbol on the first and second antenna respectively,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 ,
,  are the transmitted symbols and
are the transmitted symbols and
 is the noise on
is the noise on  receive antennas.
receive antennas.
For convenience, the above equation can be represented in matrix notation as follows:
 .
.
Equivalently,

To solve for  , The Zero Forcing (ZF) linear detector for meeting this constraint
, The Zero Forcing (ZF) linear detector for meeting this constraint  . is given by,
. is given by,
^{-1}H^H}) .
.
Using the Zero Forcing (ZF) equalization, the receiver can obtain an estimate of the two transmitted symbols  ,
,  , i.e.
, i.e.
^{-1}H^H}\left[\begin{array}y_1\\y_2\end{array}\right]) .
.
Successive Interference Cancellation with optimal ordering
In classical Successive Interference Cancellation, the receiver arbitrarily takes one of the estimated symbols, and subtract its effect from the received symbol  and
and  . However, we can have more intelligence in choosing whether we should subtract the effect of
. However, we can have more intelligence in choosing whether we should subtract the effect of  first or
first or  first. To make that decision, let us find out the transmit symbol (after multiplication with the channel) which came at higher power at the receiver. The received power at the both the antennas corresponding to the transmitted symbol
first. To make that decision, let us find out the transmit symbol (after multiplication with the channel) which came at higher power at the receiver. The received power at the both the antennas corresponding to the transmitted symbol  is,
is,
 .
.
The received power at the both the antennas corresponding to the transmitted symbol  is,
is,
 .
.
If  then the receiver decides to remove the effect of
then the receiver decides to remove the effect of  from the received vector
from the received vector  and
and  and then re-estimate
and then re-estimate  .
.
 .
.
Expressing in matrix notation,
 ,
,

Optimal way of combining the information from multiple copies of the received symbols in receive diversity case is to apply Maximal Ratio Combining (MRC). The equalized symbol is,
 .
.
Else if  the receiver decides to subtract effect of
the receiver decides to subtract effect of  from the received vector
from the received vector  and
and  , and then re-estimate
, and then re-estimate 
 .
.
Expressing in matrix notation,
 ,
,

Optimal way of combining the information from multiple copies of the received symbols in receive diversity case is to apply Maximal Ratio Combining (MRC). The equalized symbol is,
 .
.
Doing successive interference cancellation with optimal ordering ensures that the reliability of the symbol which is decoded first is guaranteed to have a lower error probability than the other symbol. This results in lowering the chances of incorrect decisions resulting in erroneous interference cancellation. Hence gives lower error rate than simple successive interference cancellation. 
Simulation Model
The Matlab/Octave script performs the following
(a) Generate random binary sequence of +1’s and -1’s.
(b) Group them into pair of two symbols and send two symbols in one time slot
(c) Multiply the symbols with the channel and then add white Gaussian noise.
(d) Equalize the received symbols with Zero Forcing criterion
(e) Find the power of received symbol from both the spatial dimensions.
(f) Take the symbol having higher power, subtract from the received symbol
(f) Perform Maximal Ratio Combining for equalizing the new received symbol
(g) Perform hard decision decoding and count the bit errors
(h) Repeat for multiple values of  and plot the simulation and theoretical results.
and plot the simulation and theoretical results.
Click here to download Matlab/Octave script for computing BER for 2×2 MIMO channel equalized by ZF-SIC with optimal ordering
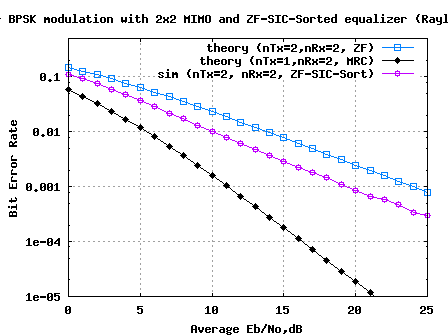
Figure: BER plot for BPSK in 2×2 MIMO equalized by ZF-SIC with optimal ordering
Observations
Compared to Zero Forcing equalization with successive interference cancellation case, addition of optimal ordering results in around 2.0dB of improvement for BER of  .
.
References
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% All rights reserved by Krishna Pillai, http://www.dsplog.com
% The file may not be re-distributed without explicit authorization
% from Krishna Pillai.
% Checked for proper operation with Octave Version 3.0.0
% Author : Krishna Pillai
% Email : krishna@dsplog.com
% Version : 1.0
% Date : 09 Novemeber 2008
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Script for computing the BER for BPSK modulation in a
% Rayleigh fading channel with 2 Tx, 2Rx MIMO channel
% Zero Forcing Equalization with Successive Interference
% Cancellation (ZF-SIC) with optimal ordering
clear
N = 10^6; % number of bits or symbols
Eb_N0_dB = [0:25]; % multiple Eb/N0 values
nTx = 2;
nRx = 2;
for ii = 1:length(Eb_N0_dB)
% Transmitter
ip = rand(1,N)>0.5; % generating 0,1 with equal probability
s = 2*ip-1; % BPSK modulation 0 -> -1; 1 -> 0
sMod = kron(s,ones(nRx,1)); %
sMod = reshape(sMod,[nRx,nTx,N/nTx]); % grouping in [nRx,nTx,N/NTx ] matrix
h = 1/sqrt(2)*[randn(nRx,nTx,N/nTx) + j*randn(nRx,nTx,N/nTx)]; % Rayleigh channel
n = 1/sqrt(2)*[randn(nRx,N/nTx) + j*randn(nRx,N/nTx)]; % white gaussian noise, 0dB variance
% Channel and noise Noise addition
y = squeeze(sum(h.*sMod,2)) + 10^(-Eb_N0_dB(ii)/20)*n;
% Receiver
% ----------
% Forming the ZF equalization matrix W = inv(H^H*H)*H^H
% H^H*H is of dimension [nTx x nTx]. In this case [2 x 2]
% Inverse of a [2x2] matrix [a b; c d] = 1/(ad-bc)[d -b;-c a]
hCof = zeros(2,2,N/nTx) ;
hCof(1,1,:) = sum(h(:,2,:).*conj(h(:,2,:)),1) ; % d term
hCof(2,2,:) = sum(h(:,1,:).*conj(h(:,1,:)),1) ; % a term
hCof(2,1,:) = -sum(h(:,2,:).*conj(h(:,1,:)),1); % c term
hCof(1,2,:) = -sum(h(:,1,:).*conj(h(:,2,:)),1); % b term
% Sorting the equalization matrix based on the channel power on each dimension
% since the second spatial dimension is equalized first, the channel
% with higher power assigned to second dimension
normSS1 = squeeze(hCof(2,2,:));
normSS2 = squeeze(hCof(1,1,:));
sortIdx = find(normSS2 < normSS1);
% sorting the H^H*H matrix
hCofSort = hCof;
hCofSort(2,2,sortIdx) = hCof(1,1,sortIdx);
hCofSort(1,1,sortIdx) = hCof(2,2,sortIdx);
hCofSort(1,2,sortIdx) = hCof(2,1,sortIdx);
hCofSort(2,1,sortIdx) = hCof(1,2,sortIdx);
hDen = ((hCofSort(1,1,:).*hCofSort(2,2,:)) - (hCofSort(1,2,:).*hCofSort(2,1,:))); % ad-bc term
hDen = reshape(kron(reshape(hDen,1,N/nTx),ones(2,2)),2,2,N/nTx); % formatting for division
hInvSort = hCofSort./hDen; % inv(H^H*H)
% sorting the H matrix
hSort = h;
hSort(:,2,sortIdx) = h(:,1,sortIdx);
hSort(:,1,sortIdx) = h(:,2,sortIdx);
% Equalization - Zero forcing
hModSort = reshape(conj(hSort),nRx,N); % H^H operation
yModSort = kron(y,ones(1,2)); % formatting the received symbol for equalization
yModSort = sum(hModSort.*yModSort,1); % H^H * y
yModSort = kron(reshape(yModSort,2,N/nTx),ones(1,2)); % formatting
yHatSort = sum(reshape(hInvSort,2,N).*yModSort,1); % inv(H^H*H)*H^H*y
% receiver - hard decision decoding on second spatial dimension
ipHat2SS = real(yHatSort(2:2:end))>0;
ipHatMod2SS = 2*ipHat2SS-1;
ipHatMod2SS = kron(ipHatMod2SS,ones(nRx,1));
ipHatMod2SS = reshape(ipHatMod2SS,[nRx,1,N/nTx]);
% new received symbol - removing the effect from second spatial dimension
h2SS = hSort(:,2,:); % channel in the second spatial dimension
r = y - squeeze(h2SS.*ipHatMod2SS);
% maximal ratio combining - for symbol in the first spatial dimension
h1SS = squeeze(hSort(:,1,:));
yHat1SS = sum(conj(h1SS).*r,1)./sum(h1SS.*conj(h1SS),1);
yHatSort(1:2:end) = yHat1SS;
yHatSort = reshape(yHatSort,2,N/2) ;
yHatSort(:,sortIdx) = flipud(yHatSort(:,sortIdx));
yHat = reshape(yHatSort,1,N);
% receiver - hard decision decoding
ipHat = real(yHat)>0;
% counting the errors
nErr(ii) = size(find([ip- ipHat]),2);
end
simBer = nErr/N; % simulated ber
EbN0Lin = 10.^(Eb_N0_dB/10);
theoryBer_nRx1 = 0.5.*(1-1*(1+1./EbN0Lin).^(-0.5));
p = 1/2 - 1/2*(1+1./EbN0Lin).^(-1/2);
theoryBerMRC_nRx2 = p.^2.*(1+2*(1-p));
close all
figure
semilogy(Eb_N0_dB,theoryBer_nRx1,'bp-','LineWidth',2);
hold on
semilogy(Eb_N0_dB,theoryBerMRC_nRx2,'kd-','LineWidth',2);
semilogy(Eb_N0_dB,simBer,'mo-','LineWidth',2);
axis([0 25 10^-5 0.5])
grid on
legend('theory (nTx=2,nRx=2, ZF)', 'theory (nTx=1,nRx=2, MRC)', 'sim (nTx=2, nRx=2, ZF-SIC-Sort)');
xlabel('Average Eb/No,dB');
ylabel('Bit Error Rate');
title('BER for BPSK modulation with 2x2 MIMO and ZF-SIC-Sorted equalizer (Rayleigh channel)');
This post attempts to build further on the MIMO equalization schemes which we have discussed -
(a) Minimum Mean Square Error (MMSE) equalization,
(b) Zero Forcing equalization with Successive Interference Cancellation (ZF-SIC) and
(c) ZF-SIC with optimal ordering.
We have learned that successive interference cancellation with optimal ordering improves the performance with Zero Forcing equalization. In this post, we extend the concept of successive interference cancellation to the MMSE equalization and simulate the performance. We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.
Brief description of 2×2 MIMO transmission, assumptions on channel model and the noise are detailed in the post on Minimum Mean Square Error (MMSE) equalization.
MMSE equalizer for 2×2 MIMO channel
Let us now try to understand the math for extracting the two symbols which interfered with each other. In the first time slot, the received signal on the first receive antenna is,
 .
.
The received signal on the second receive antenna is,
 .
.
where
 ,
,  are the received symbol on the first and second antenna respectively,
are the received symbol on the first and second antenna respectively,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 ,
,  are the transmitted symbols and
are the transmitted symbols and
 is the noise on
is the noise on  receive antennas.
receive antennas.
We assume that the receiver knows  ,
,  ,
,  and
and  . The receiver also knows
. The receiver also knows  and
and  . For convenience, the above equation can be represented in matrix notation as follows:
. For convenience, the above equation can be represented in matrix notation as follows:
 .
.
Equivalently,

The Minimum Mean Square Error (MMSE) approach tries to find a coefficient  which minimizes the criterion,
which minimizes the criterion,
 .
.
Solving,
 .
.
Using the Minimum Mean Square Error (MMSE) equalization, the receiver can obtain an estimate of the two transmitted symbols  ,
,  , i.e.
, i.e.
^{-1}H^H}\left[\begin{array}y_1\\y_2\end{array}\right]) .
.
Successive Interference Cancellation
(a) Simple
In classical Successive Interference Cancellation, the receiver arbitrarily takes one of the estimated symbols (for example the symbol transmitted in the second spatial dimension,  ), and subtract its effect from the received symbol
), and subtract its effect from the received symbol  and
and  . Once the effect of
. Once the effect of  is removed, the new channel becomes a one transmit antenna, 2 receive antenna case and can be optimaly equalized by Maximal Ratio Combining (MRC).
is removed, the new channel becomes a one transmit antenna, 2 receive antenna case and can be optimaly equalized by Maximal Ratio Combining (MRC).
(b) With optimal ordering
However, we can have more intelligence in choosing whether we should subtract the effect of  first or
first or  first. To make that decision, let us find out the transmit symbol (after multiplication with the channel) which came at higher power at the receiver. The received power at the both the antennas corresponding to the transmitted symbol
first. To make that decision, let us find out the transmit symbol (after multiplication with the channel) which came at higher power at the receiver. The received power at the both the antennas corresponding to the transmitted symbol  is,
is,
 .
.
The received power at the both the antennas corresponding to the transmitted symbol  is,
is,
 .
.
If  then the receiver decides to remove the effect of
then the receiver decides to remove the effect of  from the received vector
from the received vector  and
and 
 . Else if
. Else if  the receiver decides to subtract effect of
the receiver decides to subtract effect of  from the received vector
from the received vector  and
and  , and then re-estimate
, and then re-estimate  .
.
Once the effect of either  or
or  is removed, the new channel becomes a one transmit antenna, 2 receive antenna case and the symbol on the other spatial dimension can be optimally equalized by Maximal Ratio Combining (MRC).
is removed, the new channel becomes a one transmit antenna, 2 receive antenna case and the symbol on the other spatial dimension can be optimally equalized by Maximal Ratio Combining (MRC).
For detailed equations on the contruction of the new 2 x 1 channel using successive interference cancellation, please refer to the post on ZF-SIC with optimal ordering.
Simulation Model
The Matlab/Octave script performs the following
(a) Generate random binary sequence of +1’s and -1’s.
(b) Group them into pair of two symbols and send two symbols in one time slot
(c) Multiply the symbols with the channel and then add white Gaussian noise.
(d) Equalize the received symbols with Minimum Mean Square Error criterion
(e) Do successive interference cancellation by both classical and optimal ordering approach
(f) Perform Maximal Ratio Combining for equalizing the new received symbol
(g) Perform hard decision decoding and count the bit errors
(h) Repeat for multiple values of  and plot the simulation and theoretical results.
and plot the simulation and theoretical results.
Click here to download Matlab/Octave script for simulating BER for BPSK in 2×2 Rayleigh fading MIMO channel with MMSE-SIC equalization with and without optimal ordering

Figure; BER plot for 2×2 MIMO channel with MMSE-SIC equalization with and without optimal ordering
Observations
Compared to Minimum Mean Square Equalization with simple successive interference cancellation case, addition of optimal ordering results in around 5.0dB of improvement for BER of  .
. 
The performance is now closely matching with curve 1 transmit 2 receive antenna MRC case.
References
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% All rights reserved by Krishna Pillai, http://www.dsplog.com
% The file may not be re-distributed without explicit authorization
% from Krishna Pillai.
% Checked for proper operation with Octave Version 3.0.0
% Author : Krishna Pillai
% Email : krishna@dsplog.com
% Version : 1.0
% Date : 06 December 2008
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Script for computing the BER for BPSK modulation in a
% Rayleigh fading channel with 2 Tx, 2Rx MIMO channel
% Minimum Mean Square Error Equalization with Successive Interference
% Cancellation (ZF-SIC) with optimal ordering
clear
N = 10^6; % number of bits or symbols
Eb_N0_dB = [0:25]; % multiple Eb/N0 values
nTx = 2;
nRx = 2;
for ii = 1:length(Eb_N0_dB)
% Transmitter
ip = rand(1,N)>0.5; % generating 0,1 with equal probability
s = 2*ip-1; % BPSK modulation 0 -> -1; 1 -> 0
sMod = kron(s,ones(nRx,1)); %
sMod = reshape(sMod,[nRx,nTx,N/nTx]); % grouping in [nRx,nTx,N/NTx ] matrix
h = 1/sqrt(2)*[randn(nRx,nTx,N/nTx) + j*randn(nRx,nTx,N/nTx)]; % Rayleigh channel
n = 1/sqrt(2)*[randn(nRx,N/nTx) + j*randn(nRx,N/nTx)]; % white gaussian noise, 0dB variance
% Channel and noise Noise addition
y = squeeze(sum(h.*sMod,2)) + 10^(-Eb_N0_dB(ii)/20)*n;
% Receiver
% ----------
% Forming the MMSE equalization matrix W = inv(H^H*H + sigma^2*I)*H^H
% H^H*H is of dimension [nTx x nTx]. In this case [2 x 2]
% Inverse of a [2x2] matrix [a b; c d] = 1/(ad-bc)[d -b;-c a]
hCof = zeros(2,2,N/nTx) ;
hCof(1,1,:) = sum(h(:,2,:).*conj(h(:,2,:)),1) + 0*10^(-Eb_N0_dB(ii)/10); % d term
hCof(2,2,:) = sum(h(:,1,:).*conj(h(:,1,:)),1) + 0*10^(-Eb_N0_dB(ii)/10); % a term
hCof(2,1,:) = -sum(h(:,2,:).*conj(h(:,1,:)),1); % c term
hCof(1,2,:) = -sum(h(:,1,:).*conj(h(:,2,:)),1); % b term
for kk = 1:2
if kk == 1
sortIdx = [];
hCof(1,1,:) = sum(h(:,2,:).*conj(h(:,2,:)),1) + 10^(-Eb_N0_dB(ii)/10); % d term
hCof(2,2,:) = sum(h(:,1,:).*conj(h(:,1,:)),1) + 10^(-Eb_N0_dB(ii)/10); % a term
hCof(2,1,:) = -sum(h(:,2,:).*conj(h(:,1,:)),1); % c term
hCof(1,2,:) = -sum(h(:,1,:).*conj(h(:,2,:)),1); % b term
elseif kk == 2
% Sorting the equalization matrix based on the channel power on each dimension
% since the second spatial dimension is equalized first, the channel
% with higher power assigned to second dimension
normSS1 = squeeze(hCof(2,2,:));
normSS2 = squeeze(hCof(1,1,:));
sortIdx = find(normSS2 < normSS1);
end
% sorting the H^H*H + sigma^2*I matrix
hCofSort = hCof;
if ~isempty(sortIdx)
hCofSort(2,2,sortIdx) = hCof(1,1,sortIdx) + 10^(-Eb_N0_dB(ii)/10);;
hCofSort(1,1,sortIdx) = hCof(2,2,sortIdx) + 10^(-Eb_N0_dB(ii)/10);;
hCofSort(1,2,sortIdx) = hCof(2,1,sortIdx);
hCofSort(2,1,sortIdx) = hCof(1,2,sortIdx);
end
hDen = ((hCofSort(1,1,:).*hCofSort(2,2,:)) - (hCofSort(1,2,:).*hCofSort(2,1,:))); % ad-bc term
hDen = reshape(kron(reshape(hDen,1,N/nTx),ones(2,2)),2,2,N/nTx); % formatting for division
hInvSort = hCofSort./hDen; % inv(H^H*H)
% sorting the H matrix
hSort = h;
if ~isempty(sortIdx)
hSort(:,2,sortIdx) = h(:,1,sortIdx);
hSort(:,1,sortIdx) = h(:,2,sortIdx);
end
% Equalization - Zero forcing
hModSort = reshape(conj(hSort),nRx,N); % H^H operation
yModSort = kron(y,ones(1,2)); % formatting the received symbol for equalization
yModSort = sum(hModSort.*yModSort,1); % H^H * y
yModSort = kron(reshape(yModSort,2,N/nTx),ones(1,2)); % formatting
yHatSort = sum(reshape(hInvSort,2,N).*yModSort,1); % inv(H^H*H)*H^H*y
% receiver - hard decision decoding on second spatial dimension
ipHat2SS = real(yHatSort(2:2:end))>0;
ipHatMod2SS = 2*ipHat2SS-1;
ipHatMod2SS = kron(ipHatMod2SS,ones(nRx,1));
ipHatMod2SS = reshape(ipHatMod2SS,[nRx,1,N/nTx]);
% new received symbol - removing the effect from second spatial dimension
h2SS = hSort(:,2,:); % channel in the second spatial dimension
r = y - squeeze(h2SS.*ipHatMod2SS);
% maximal ratio combining - for symbol in the first spatial dimension
h1SS = squeeze(hSort(:,1,:));
yHat1SS = sum(conj(h1SS).*r,1)./sum(h1SS.*conj(h1SS),1);
yHatSort(1:2:end) = yHat1SS;
yHatSort = reshape(yHatSort,2,N/2) ;
if ~isempty(sortIdx)
yHatSort(:,sortIdx) = flipud(yHatSort(:,sortIdx));
end
yHat = reshape(yHatSort,1,N);
% receiver - hard decision decoding
ipHat = real(yHat)>0;
% counting the errors
nErr(kk,ii) = size(find([ip- ipHat]),2);
end
end
simBer = nErr/N; % simulated ber
EbN0Lin = 10.^(Eb_N0_dB/10);
theoryBer_nRx1 = 0.5.*(1-1*(1+1./EbN0Lin).^(-0.5));
p = 1/2 - 1/2*(1+1./EbN0Lin).^(-1/2);
theoryBerMRC_nRx2 = p.^2.*(1+2*(1-p));
close all
semilogy(Eb_N0_dB,theoryBer_nRx1,'bp-','LineWidth',2);
hold on
semilogy(Eb_N0_dB,theoryBerMRC_nRx2,'kd-','LineWidth',2);
semilogy(Eb_N0_dB,simBer(1,:),'mo-','LineWidth',2);
semilogy(Eb_N0_dB,simBer(2,:),'gp-','LineWidth',2);
axis([0 25 10^-5 0.5])
grid on
legend('theory (nTx=2,nRx=2, ZF)', 'theory (nTx=1,nRx=2, MRC)', 'sim (nTx=2, nRx=2, MMSE-SIC)','sim (nTx=2, nRx=2, MMSE-SIC-Sort)');
xlabel('Average Eb/No,dB');
ylabel('Bit Error Rate');
title('BER for BPSK modulation with 2x2 MIMO and MMSE-SIC equalizer (Rayleigh channel)');
In the past, we had discussed several posts on two transmit two receive MIMO communication, where the transmission was based on V-BLAST. The details about V-BLAST can be read from the landmark paper V-BLAST: An architeture for realizing very high data rates over the rich scattering wireless channel – P. W. Wolniansky, G. J. Foschini, G. D. Golden, R. A. Valenzuela. We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.

Figure: 2 transmit 2 receive MIMO channel
V-BLAST transmission for 2×2 MIMO channel
In a 2×2 MIMO channel, probable usage of the available 2 transmit antennas can be as follows:
1. Consider that we have a transmission sequence, for example 
2. In normal transmission, we will be sending  in the first time slot,
in the first time slot,  in the second time slot,
in the second time slot,  and so on.
and so on.
3. However, as we now have 2 transmit antennas, we may group the symbols into groups of two. In the first time slot, send  and
and  from the first and second antenna. In second time slot, send
from the first and second antenna. In second time slot, send  and
and  from the first and second antenna, send
from the first and second antenna, send  and
and  in the third time slot and so on.
in the third time slot and so on.
4. Notice that as we are grouping two symbols and sending them in one time slot, we need only  time slots to complete the transmission – data rate is doubled !
time slots to complete the transmission – data rate is doubled ! 
5. This forms the simple explanation of a probable MIMO transmission scheme with 2 transmit antennas and 2 receive antennas.
Other Assumptions
1. The channel is flat fading – In simple terms, it means that the multipath channel has only one tap. So, the convolution operation reduces to a simple multiplication. For a more rigorous discussion on flat fading and frequency selective fading, may I urge you to review Chapter 15.3 Signal Time-Spreading from [DIGITAL COMMUNICATIONS: SKLAR]
2. The channel experience by each transmit antenna is independent from the channel experienced by other transmit antennas.
3. For the  transmit antenna to
transmit antenna to  receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number
receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number  . As the channel under consideration is a Rayleigh channel, the real and imaginary parts of
. As the channel under consideration is a Rayleigh channel, the real and imaginary parts of  are Gaussian distributed having mean
are Gaussian distributed having mean  and variance
and variance  .
.
4. The channel experienced between each transmit to the receive antenna is independent and randomly varying in time.
5. On the receive antenna, the noise has the Gaussian probability density function with
has the Gaussian probability density function with
 with
with  and
and  .
.
7. The channel  is known at the receiver.
is known at the receiver.
System Model
The received signal on the first receive antenna is,
 .
.
The received signal on the second receive antenna is,
 .
.
where
 ,
,  are the received symbol on the first and second antenna respectively,
are the received symbol on the first and second antenna respectively,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 is the channel from
is the channel from  transmit antenna to
transmit antenna to  receive antenna,
receive antenna,
 ,
,  are the transmitted symbols and
are the transmitted symbols and
 is the noise on
is the noise on  receive antennas.
receive antennas.
We assume that the receiver knows  ,
,  ,
,  and
and  . The receiver also knows
. The receiver also knows  and
and  . The unknown s are
. The unknown s are  and
and  . Two equations and two unknowns. Can we solve it? Answer is YES.
. Two equations and two unknowns. Can we solve it? Answer is YES. 
For convenience, the above equation can be represented in matrix notation as follows:
 .
.
Equivalently,

Receiver structures
The zero forcing approach tries to find a matrix  which satisfies
which satisfies  . The Zero Forcing (ZF) linear detector for meeting this constraint is given by,
. The Zero Forcing (ZF) linear detector for meeting this constraint is given by,
^{-1}H^H}) .
.
The Minimum Mean Square Error (MMSE) approach tries to find a coefficient  which minimizes the criterion,
which minimizes the criterion,
 .
.
Solving,
 .
.
Using the Zero Forcing (ZF) equalization approach described above, the receiver can obtain an estimate of the two transmitted symbols  ,
,  , i.e.
, i.e.
^{-1}H^H}\left[\begin{array}y_1\\y_2\end{array}\right]) .
.
Take one of the estimated symbols (for example  ) and subtract its effect from the received vector
) and subtract its effect from the received vector  and
and  , i.e.
, i.e.
 .
.
Expressing in matrix notation,
 ,
,

The above equation is same as equation obtained for receive diversity case. Optimal way of combining the information from multiple copies of the received symbols in receive diversity case is to apply Maximal Ratio Combining (MRC).
The equalized symbol is,
 .
.
This forms the simple explanation for Zero Forcing Equalizer with Successive Interference Cancellation (ZF-SIC) approach.
In classical Successive Interference Cancellation, the receiver arbitrarily takes one of the estimated symbols, and subtract its effect from the received symbol  and
and  . However, we can have more intelligence in choosing whether we should subtract the effect of
. However, we can have more intelligence in choosing whether we should subtract the effect of  first or
first or  first. To make that decision, let us find out the transmit symbol (after multiplication with the channel) which came at higher power at the receiver. The received power at the both the antennas corresponding to the transmitted symbol
first. To make that decision, let us find out the transmit symbol (after multiplication with the channel) which came at higher power at the receiver. The received power at the both the antennas corresponding to the transmitted symbol  is,
is,
 .
.
The received power at the both the antennas corresponding to the transmitted symbol  is,
is,
 .
.
If  then the receiver decides to remove the effect of
then the receiver decides to remove the effect of  from the received vector
from the received vector  and
and  and then re-estimate
and then re-estimate  . Else if
. Else if  the receiver decides to subtract effect of
the receiver decides to subtract effect of  from the received vector
from the received vector  and
and  , and then re-estimate
, and then re-estimate  .
.
Using the Minimum Mean Square Error (MMSE) equalization, the receiver can obtain an estimate of the two transmitted symbols  ,
,  , i.e.
, i.e.
^{-1}H^H}\left[\begin{array}y_1\\y_2\end{array}\right]) .
.
If  then the receiver decides to remove the effect of
then the receiver decides to remove the effect of  from the received vector
from the received vector  and
and 
 . Else if
. Else if  the receiver decides to subtract effect of
the receiver decides to subtract effect of  from the received vector
from the received vector  and
and  , and then re-estimate
, and then re-estimate  .
.
Once the effect of either  or
or  is removed, the new channel becomes a one transmit antenna, 2 receive antenna case and the symbol on the other spatial dimension can be optimally equalized by Maximal Ratio Combining (MRC).
is removed, the new channel becomes a one transmit antenna, 2 receive antenna case and the symbol on the other spatial dimension can be optimally equalized by Maximal Ratio Combining (MRC).
The Maximum Likelihood receiver tries to find  which minimizes,
which minimizes, 

Since the modulation is BPSK, the possible values of  is +1 or -1 Similarly
is +1 or -1 Similarly  also take values +1 or -1. So, to find the Maximum Likelihood solution, we need to find the minimum from the all four combinations of
also take values +1 or -1. So, to find the Maximum Likelihood solution, we need to find the minimum from the all four combinations of  and
and  .
.




The estimate of the transmit symbol is chosen based on the minimum value from the above four values i.e
if the minimum is  ,
,
if the minimum is  ,
,
if the minimum is  and
and
if the minimum is  .
.
Simulation Results
The plot embedded below captures BER for 2 transmit 2 receive MIMO V-BLAST ttansmission/reception for BPSK modulation in a flat fading independent Rayleigh channel, for the different equalizer structures discussed above.
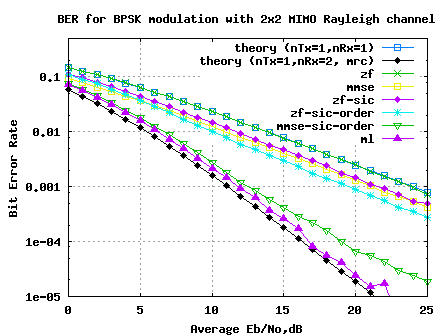
Figure: BER plot for 2 transmit 2 receive MIMO channel for BPSK modulation
Observations
1. The BER curve with ZF equalization for 2×2 MIMO channel is identical to BER plot for 1 transmit 1 receive system
2. Ordered variant of successive interference cancellation shows better performance than the simple successive interference cancellation
3. MMSE equalization with ordered successive interference cancellation provides performance which is slightly poorer than ML.
4. With ML equalization, we come close to the performance of 1 transmit 2 receive MRC case. We gain both throughput gain and diversity gain.
Reference
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt
V-BLAST: An architeture for realizing very high data rates over the rich scattering wireless channel – P. W. Wolniansky, G. J. Foschini, G. D. Golden, R. A. Valenzuela.
.
.
,
are the received symbol on the first and second antenna respectively,
is the channel from
transmit antenna to
receive antenna,
is the channel from
transmit antenna to
receive antenna,
is the channel from
transmit antenna to
receive antenna,
is the channel from
transmit antenna to
receive antenna,
,
are the transmitted symbols and
is the noise on
receive antennas.
.
, The Zero Forcing (ZF) linear detector for meeting this constraint
. is given by,
.
,
, i.e.
.
and
. However, we can have more intelligence in choosing whether we should subtract the effect of
first or
first. To make that decision, let us find out the transmit symbol (after multiplication with the channel) which came at higher power at the receiver. The received power at the both the antennas corresponding to the transmitted symbol
is,
.
is,
.
then the receiver decides to remove the effect of
from the received vector
and
and then re-estimate
.
.
,
.
the receiver decides to subtract effect of
from the received vector
and
, and then re-estimate
.
,
.
![]()
and plot the simulation and theoretical results.
.






